
unconstained optimization of smooth function
- line search method
- Newton direction
- Quasi-Newton
Rates Of Convergence
- \(Q-linear\) \[\frac{||x_{k+1}-x_{k}^{*}||}{||x_{k}-x^*||}\leq r \qquad for\; all\; k\; sufficiently\; large\]
- \(Q-superlinear\) \[\lim_{k \to \infty}\frac{||x_{k+1}-x_{k}^{*}||}{||x_{k}-x^*||}=0\]
- \(Q-quadratic\) \[\frac{||x_{k+1}-x_{k}^{*}||}{||x_{k}-x^*||^2}\leq M \qquad for\; all\; k\; sufficiently\; large\]
第二章习题 #### 2.1 \[\nabla f(x)=\begin{bmatrix} 400x_{1}^{3}-400x_{2}x_2+2x_{1}-2 \\ 200(x_{2}-x_1^2) \end{bmatrix}\] \[\nabla ^2 f(x)=\begin{bmatrix} 1200x_1^2-400x_1x_2+2x_1-2 & -400x_1\\ -400x_1&200 \end{bmatrix}\] let \(\nabla f(x) =0\),we can get that \[\begin{cases} 400x_{1}^{3}-400x_{2}x_2+2x_{1}-2=0\\ 200(x_{2}-x_1^2)=0 \end{cases} \] got the only solution \(x^*=(1,1)^T\) ,cause the \(\nabla ^2f(x)\) is positive definite,the \(x^*\) is the only local minimizer of this function.
2.2
coutour 等高线?
\(\nabla f(x)= \begin{bmatrix} 2x_1+8 \\ 12-4x_2 \end{bmatrix}\) the only stationary of \(f(x)=8x_1+12x_2+x_1^2-2x_2^2\) is \(x^*=(-4,3)^T\) ##### 等高线画法不太了解  使用python得到如下结果
使用python得到如下结果 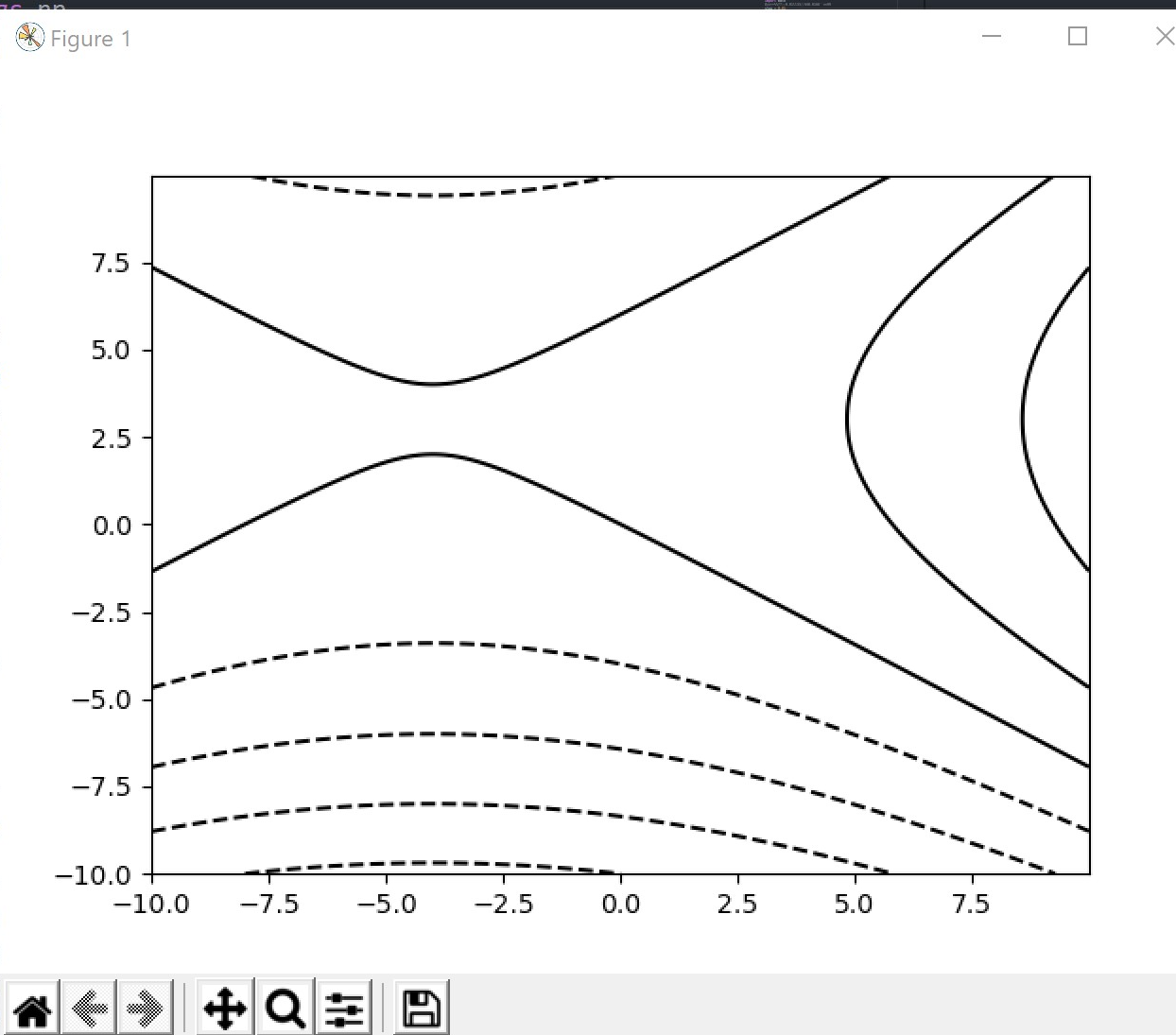
2.3
\[a^Tx=\begin{bmatrix} a_1&a_2 \cdots a_n \end{bmatrix} * \begin{bmatrix} x_1 \\ x_2\\ \vdots\\ x_n \end{bmatrix}=\sum_{i=1}^{n}a_ix_i\] so \(\nabla f_1(x)=\begin{bmatrix} a_1 \\ a_2 \\ \vdots \\ a_n\end{bmatrix}=a\)
\(\nabla ^2f_1(x)=0\) \[x^TAx=\begin{bmatrix} x_1 & x_2 & \cdots & x_n\end{bmatrix}
\begin{bmatrix} A_{11} &A_{12} &\cdots & A_{1n}\\ A_{21}&\ddots \\ \vdots \\ A_{2n} \end{bmatrix}\begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n\end{bmatrix}\\=\sum_{j=1}^{n}\sum_{i=1}^{n}A_{ij}x_ix_j\] \(\sum_{j=1}^{n}\sum_{i=1}^{n}A_{ij}x_ix_j=x_{index}\sum_{i={1}}^{n}A_{ij}x_i+x_{index}\sum_{j={1}}^{n}A_{ij}x_i+\sum_{j\not={index}}^{n}\sum_{i=1}^{n}A_{ij}x_ix_j+\sum_{j=1}^{n}\sum_{i\not={index}}^{n}A_{ij}x_ix_j\)
so \(\nabla f_2(x)\)